A Dynamic Programming Beginner Guide
Hey folks! Well if you clicked on this article then I'm guessing that you might have some struggles with dynamic programming or you might understand it but not get the full picture.
In this article, I'll try my best to cover how I understood dynamic programming and some tips and tricks I've learned from surfing different blog posts and youtube videos. So without further or do let's get started.
Just a note that everything written in this article is based on my experience and how I got a grip on dynamic programming. It might be different for you depending on how much you understand it already I'm by no means a coach or anything like that I just thought I'd share what I've learned to maybe help make it easier for beginners to get the grip faster.
Hang on there. What even is Dynamic Programming?
Before understanding dynamic programming we need to understand how we naively approach any problem. I'll be taking examples from Leetcode and linking them in this article and explaining step by step my thought process.
Let's for example take a simple dynamic programming category problem which is Min Cost Climbing Stairs, I'd encourage you to read the problem before continuing.
A simple approach to calculating the minimum given that you can either climb one or two steps when paying the cost (again I'd encourage you to read the problem before continuing) is to simply calculate all the combinations of all possible alterations you can make to reach the top. Calculating all possible combinations is simply referred to as The Brute Force Approach which does get you the right answer, however, performance wise it won't get accepted on Leetcode or probably in any interview you do. Let's explain why brute force is not optimal below;
The brute force approach for the problem mentioned is going to be recursive since we need to get all different combinations; for example, if I start at index 0 I can go to either index 1 or index 2, and when reaching index 1 I can go to either index 2 or index 3 and so on. So to calculate all possible calculations we need to consider all the cases and execute all cases recursively. An approach like this can best be explained with what is called a decision tree.
Let's work with an example of the following
cost = [10,15,20]
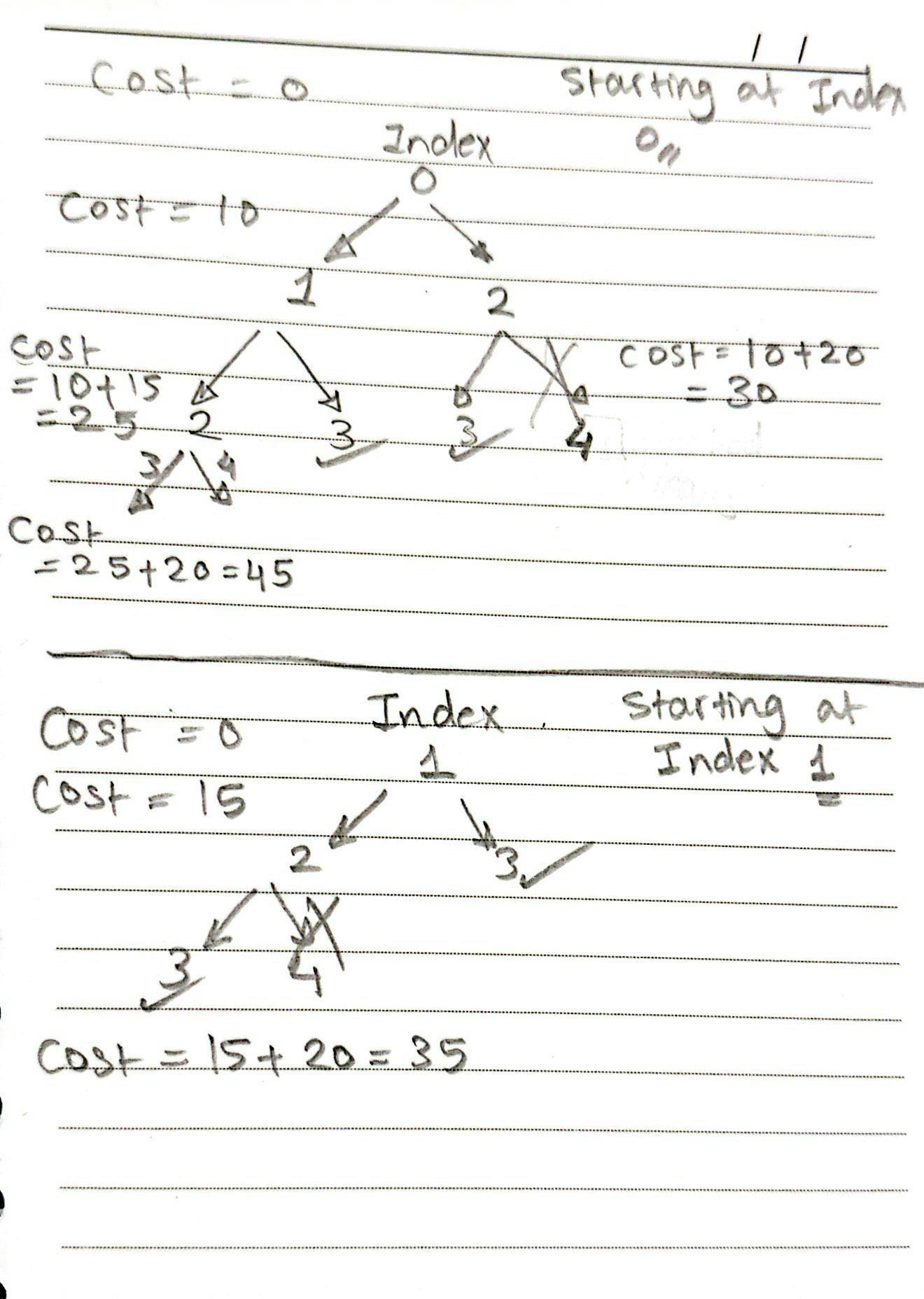
Since the problem states that you can start from index 0 or 1, we calculate all the possible combinations starting from index 0 and starting from index 1 as shown in the decision tree above.
When we reach index 3 we are done since the last element of the array has an index of 2 and by reaching 3 that means we have arrived at the top floor.
Why is this solution not optimal & Dynamic Programming intro
This solution is not optimal because if we look closely at the decision tree, we'll realize that there is a lot of repeated work going on, but what does repeated work even mean? let's analyze.
When we start at index 0 we can either reach index 1 or index 2 right? then we recursively call the subproblem which either starts from index 1 or index 2. Well if we examine it carefully we'll realize that one subproblem which is when we start at index 2 will get executed twice, Since from index 1 we have a subproblem that either goes to index 2 or index 3 as well as having an option to directly go to index 2 from index 0. So the subproblem starting at the stair of index 2 will get executed again for no reason since we should have already calculated it from the first execution. This is usually called repeated work and here is where Dynamic Programming comes in handy. What Dynamic Programming does is it will cache the execution of the index 2 subproblem and whenever we encounter a subproblem that starts from index 2, we'll just return the cached value instead of executing it all over again for it to return the same value. Effectively reducing the time complexity from O(2**n) to O(n).
Dynamic Programming effectively works on caching repeated work and this would greatly optimize a problem like this since we only have to calculate each step once and return the cached value whenever we land on some common step later on.
Dynamic Programming has different techniques and is a deep topic, this article is just a simple guide on how to make your brain think effectively when encountering a DP Problem. Always try to look out for repeated work and cache it effectively.
Dynamic Programming Techniques
There are several ways of solving DP Problems, But two of the most used are either Top Down or Bottom Up approaches and we'll discuss the difference between them and how to convert from top-down to bottom-up.
Top Down Technique
This is usually the recursive technique which is easier to come up with in most questions, here's how to think top-down style;
1- Apply the brute force solution recursively
2- Try to locate any repeated work usually by drawing a decision tree or thinking about the problem carefully
3- Try to understand what should be cached and how effectively would the cached parameter(s) reduce execution time.
4- Cache and you're good to go.
Let's do these steps one by one with the given Leetcode example.
Apply the brute force solution recursively
def minCostClimbingStairs(self, cost: List[int]) -> int:
ln = len(cost)
def dfs(index):
if index >= ln:
return 0
return cost[index] + min(dfs(index+1), dfs(index + 2))
return min(dfs(0), dfs(1))
This is the recursive brute force approach, a function that takes the index we're at as a parameter and our base case is whenever we reach the end of the array which is the top we return 0, the return value represents the cost for the subproblem that starts from the specified index.
The complexity for this approach would be (2**n) where 2 is the number of decisions we make per one subproblem (either go up by 1 index or 2) and we do this till we reach the end of the array which is of length n.
Try to locate any repeated work usually by drawing a decision tree or thinking about the problem carefully
Here as we discussed before the repeated work is whenever we have a start index that has already been calculated. So our cache parameter will be the index we're at so whenever we visit this index again we return our cached value instead of re-execution.
def minCostClimbingStairs(self, cost: List[int]) -> int:
ln = len(cost)
dp = {}
def dfs(index):
if index >= ln:
return 0
if index in dp:
return dp[index]
ans = cost[index] + min(dfs(index+1), dfs(index + 2))
dp[index] = ans
return dp[index]
return min(dfs(0), dfs(1))
The cache is usually a hashmap of some sort for recursive solutions, we just cache the calculated value and whenever the value exists in the hashmap we return it immediately.
The time complexity for this solution goes down to O(n) which is a linear approach.
All good but can we do better?
Usually, recursive solutions are more readable and they're fine. However, there are more optimal solutions regarding memory usage. Recursion usually uses up stack memory due to the number of function calls made which can be a bit overhead. A solution to this is another approach called the bottom-up which is not recursive but iterative as we'll see below.
Bottom Up Technique
The bottom-up technique is usually an iterative approach where we get rid of the stack memory used by recursion and that can provide better optimization for our problem.
Converting from Top Down to Bottom Up might be tricky at first. But when you understand and practice trying it things will get a lot easier.
Bottom-up approaches are usually a 1D or 2D array depending on the problem, The array (we'll call it DP) is usually the cache we're talking about. But instead of recursively going all the way down the decision tree and then back up, we start from the bottom of the tree and work our way up since we need the answers to the subproblems down there first anyways.
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost) + 2)
for i in range(len(cost) - 1,-1,-1):
dp[i] = cost[i] + min(dp[i+1], dp[i+2])
return min(dp[0], dp[1])
Every index in the array DP represents the optimal cost from starting at that index till reaching the top.
Remember our base case when we said if we exceed the length of the array we're done? that's why we added 2 to the length of the DP array. Because we're going from the bottom and working our way backward, starting from the last index what is the minimum value to reach the top? it's its own cost only. The + 2 added accounts for an out-of-range error that might happen when we're at the last index. since we can either go up by 1 or 2 and the last index + either 1 or 2 exceeds the length of our costs array.
We loop in reverse since it's a bottom-up approach starting from the base case and making the way to the first stair. Notice how the following two lines are similar
# Top Down
ans = cost[index] + min(dfs(index+1), dfs(index + 2))
# Bottom Up
dp[i] = cost[i] + min(dp[i+1], dp[i+2])
This is called the recurrence relation. In simpler terms what is the relation of all the subproblems together? all subproblems work together to solve the bigger problem so what is the relation that connects them all together?
Notice how we need to calculate higher index numbers to be able to calculate the index we're standing at right now? For example, if we are at index 1 we need to calculate the subproblems of index 2 and 3 so we can have an answer for the index 1 subproblem? That's why bottom-up is more efficient since it calculates them first and moves backward so whenever we reach index 1 we already calculated indexes 2 and 3 and we're ready to just return the cached value. While in the Top Down approach we need to go depth-first style into the bottom of the tree to be able to calculate index 2 then do another depth-first to either calculate index 3 from scratch or return a cached value if found.
Finally, we return the minimum of either the first or second values in the array DP since we can either start from index 0 or index 1.
Summary and some random tips
I hope you understood or benefited anything from this simple beginner article explaining the benefits of dynamic programming.
One tip I would recommend is just to practice. It will never be that clear at first and it needs consistency to be able to train your brain how to think and handle different dynamic programming problems. I would recommend heading over to Leetcode and going through the easy problems first then working your way to much harder ones. There are a lot of different types of Dynamic Programming problem styles and I recommend this Article that goes in-depth into Dynamic Programming concepts and different problem styles.
Also, I would recommend watching NeetCode's DP course. Not only that but he also has a youtube solution for most Leetcode DP Problems. This guy is a living legend and he has helped me so much I can't recommend him enough!
Always try to find the recurrence relation, catch any repeated work and try to optimize.
Thanks and till the next one guys!
